Reaction rates can be informative, such as when you want to know how fast a drug will be metabolized in the body or how fast it takes for an oral medication to dissolve into the bloodstream. However, the quality of the information that can be obtained from a study of reaction rates will always depend on the skill of the experimenter. Theory can never replace the insight that can be obtained from work in the laboratory.
In this article, we will dive into the concept of kinetics, such as reaction rates, chemical equilibrium, the rate constant, and the reaction order.
- Reaction Rates - We will consider reaction rates in the context of instantaneous rates.
- Rate Law - We discuss the experimental determination of the rate of reaction.
- Instantaneous Rate - We discuss the experimental determination of the rate of reaction in greater detail.
- Reaction Order and Rate Constant - We go over the experimental determination of the reaction order with a specific example.
Kinetics Meaning
Let's start by looking at the meaning of kinetics:
Kinetics is the branch of chemistry that focuses on reaction rates
Reaction rate is the rate at which a chemical reaction proceeds
When the rate of the reaction leading to products, the forward reaction, is equal to the rate of the reaction leading back to reactants, reverse reaction, we have a system in chemical equilibrium.
A system at equilibrium will occur when the concentration of components does not change with time.
The rates of reaction for a system at chemical equilibrium are not zero.
The chemical equilibrium constant (Keq) shows the relationship between products and reactants at equilibrium.
For a general reaction:
$$a\textbf{A}+b\textbf{B} \rightleftarrows c\textbf{AB}$$
The equilbrium constant is:
$$K_{eq}=\frac{[\textbf{AB}]^c}{[\textbf{A}]^a[\textbf{B}]^b}$$
Graphically, the equilibrium constant can be viewed as a reaction limit in which the concentration of products and reactants does not change with time. For example, consider a reaction of the type
\(a\textbf{A}+b\textbf{B}\rightleftarrows c\textbf{AB}\), that displays the following changes in the concentrations of reactants and products versus time:
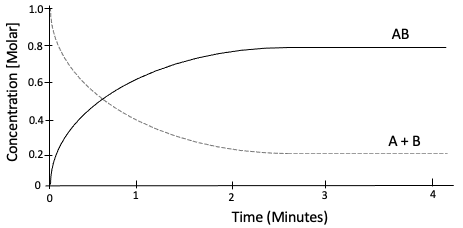Figure 1: Reaction that has reached equilibrium.
As can be seen in figure 1, the concentrations of products over reactants do not seem to change at around the 4-minute mark.
However, in the laboratory, it is often not practical to follow the progress of a chemical reaction over an extended length of time. This is true for a variety of technical and theoretical reasons which we will not discuss in detail. Rather, we shall go over instantaneous rates of reaction which bypasses the problems associated with determining the equilibrium constant directly.
Kinetics Definition
We emphasize the following important fact; The rate of any chemical reaction can be determined by measuring the instantaneous reaction rate.
Taking a step back, we note that a reaction rate can be defined as follows:
The rates of chemical reaction correspond to how fast components are changing in a dynamic system.
The reaction rate, or speed at which a chemical reaction occurs, differs substantially for different reaction conditions, types of reactants, and stability of products.
Some reactions occur almost instantly, while others may take a very long time, even years, to reach a state in which the concentrations of products and reactants do not change.
The change in the concentration of products or reactants per unit time is referred to as the reaction rate.
We define the term rate law as follows:
Rate Law - is a mathematical expression that relates the rate of reaction to changes in the concentrations of either reactants or products.
Now, we define the instantaneous rate as follows:
- To measure the instantaneous rate of any reaction we consider the change in the concentration of a component of the reaction system over short periods and over an appropriate interval of time. (For instance, we could measure the increase of the concentration of the product, AB, every 2 seconds for a total interval of 10 seconds, please see figures 5 & 6, for examples)
- If the plot of the concentration of a reaction component, over an appropriate time interval, yields a linear curve, then the slope of the graph is equal to the instantaneous reaction rate.
The details of the steps involved to determine the instantaneous rate of a reaction are discussed below.
Chemical Kinetics
Consider, the formation of the product (AB) for a chemical system consisting of reactants A and B. In the forward reaction, reactants A and B decrease while the formation of the product AB increases:
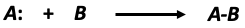Figure 2: Hypothetical forward chemical reaction.
Graphically, the above hypothetical forward chemical reaction can be depicted as:
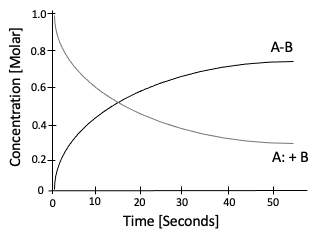Figure 3: Hypothetical reaction profile where the product AB, increases whilst A and B, decrease.
Let's consider the hypothetical forward reaction in greater detail,
$$a\textbf{A}+b\textbf{B} \rightarrow c\textbf{AB}$$
where,
For any point in time, we can write an expression for the rate of the forward reaction as:
$$Rate=\frac{-1}{a}\frac{d\textbf[A]}{dt}=\frac{-1}{b}\frac{d[B]}{dt}=\frac{1}{c}\frac{d[AB]}{dt}$$
where,
The negative sign denotes a decrease in the concentrations of the reactants [A] and [B]
The change in the concentrations with time, of all components, are denoted by the symbol,\(\frac{d[...]}{dt}\).
We can translate the rate law into words as, 'the decrease per second in the concentration of reactant A, is equal to the decrease in the concentration per second in the concentration of reactant B, which are both equal to the increase per second in the concentration of the product AB.
In particular, for any point in time, we can determine the reaction rate by determining any one of the equations of the rate law because all of the changes in the concentrations of the components are proportionate to one another.
Thus, we can monitor the rate of change of any of the reaction components to arrive at the rate law:
$$Rate=\frac{-1}{a}\frac{d[\textbf{A}]}{dt}\,, or ,\,\,Rate=\frac{-1}{b}\frac{d[\textbf{B}]}{dt}\,, or, \,\,Rate=\frac{1}{c}\frac{d[\textbf{AB}]}{dt}$$
The rate law for the formation of water: For example, consider the forward reaction for the formation of water from hydrogen and oxygen gas:
$$2H_2 \left( g \right) +O_2 \left( g \right) \rightarrow 2H_2O \left( l \right) $$
where, \(a=2\), \(\textbf{A}=H_2\) ; \(b=1\), \(\textbf{B}=O_2\) ; and \(c=2\), \(\textbf{AB}=H_2O\).
Then, at any point in time, the rate law for the forward chemical reaction corresponding to the formation of water would be:
$$Rate=\frac{-1}{2}\frac{d[H_2]}{dt}\,, or ,\,\,Rate=\frac{-1}{1}\frac{d[O_2]}{dt}\,, or ,\,\,Rate=\frac{1}{2}\frac{H_2O}{dt}$$
Instantaneous Rate
Let's consider in greater detail the plot of the concentration of a product over time; for example, consider the product of the reaction system: \(a\textbf{A}+b\textbf{B} \rightarrow c\textbf{AB}\).
Figure 4: Plot of the formation of product, AB.
Now, if we focus in on the first ten seconds of the graph for the production of, AB , we find:
Figure 5: Zooming in on the first ten seconds of the reaction producing the product, AB .
The instantaneous rate is the slope of the curve fitted to a scatter plot of the concentration of any one of the reaction components versus time.
Over the course of a chemical reaction, the reaction rate tends to decrease as reactants are consumed.
The actual rate, measured as the increase in the concentration of the product, varies continuously over the full course of a reaction.
An instantaneous rate taken near the beginning of a reaction, \(t=0\), is called the initial rate.
At the beginning of the reaction, the initial rate of the formation of products is greatest.
When we measure the instantaneous rate of a reaction we can measure either the changes in the concentrations of reactants or products. Particularly, useful applications of the measurements of instantaneous rates are:
The measurement of the initial rate of the formation of products is a common method used to determine enzymatic activity.
The measurement of the initial rate of the consumption of reactants is commonly used in chemistry to obtain the reaction order of reactant components in an effort to figure out the reaction mechanism.
Reaction Order and Rate Constant
As we noted above, the measurement of the initial rate of the consumption of reactants is commonly used in chemistry to obtain the reaction order.
Reaction order is the relationship between the reaction rate and the concentration of the species in the reaction
That is, we now switch the focus of the determination of the initial rate to the consumption, or decrease in the concentration, of reactants.
Figure 6: Zooming in on the first ten seconds of the reaction consuming the reactant, A or B .
When using the initial rates of the consumption of reactants, the general rate law takes the form:
$$Rate=k[Reactant 1]^m\cdot[Reactant 2]^n\cdot\cdot\cdot[Reactant N]^z$$
Where,
The rate law, Rate, is given in dimensions of molarity per second (M/s)
The rate constant (k) is a constant of proportionality and the reaction involves any number of reactants: Reactant 1, Reactant 2, ... ,Reactant N.
In addition, the concentrations of each of the reactants are raised to various powers: m, n, ... , z ; which correspond to the reaction order with respect to that particular reactant.
Kinetic Energy Examples
For instance, the rate law for the oxidation of the bromide ion by the bromate ion in acidic solution, \(5{Br}^- \left( {aq} \right)+{BrO_3}^- \left( {aq} \right)+6{H_2}^+ \left( {aq} \right) \rightarrow 3Br_2 \left( {aq} \right)+3H_2O \left( l \right) \), is given by:
$$Rate=k[{Br_2}^-]^1\cdot[{BrO_3}^-]^1\cdot[H^+]^2$$
Thus, the reaction order with respect to the bromide ion, \(Br^-\), is first order, the reaction order with respect to the bromate ion, \({BrO_3}^-\), is also first order and the reaction order with respect to acid, \(H^+\), is second order.
The overall reaction order is given by summing all of the reaction orders for all reactants: For Example, the reaction order for the rate law, \(Rate=k[{Br_2}^-]^1\cdot[{BrO_3}^-]^1\cdot[H^+]^2\), is:
$$Reaction\,Order=1+1+2=4$$
First-order Kinetics Formula
Consider the following reaction:
$$2N_2O_5 \left( g \right) \rightarrow 4NO_2 \left( g \right) +O_2 \left( g \right) $$
We run three experiments at constant temperature, in which, we measure the initial rate for the decomposition of the reactant, \(N_2O_5\). In particular, we double the initial concentration of, \(N_2O_5\), for each subsequent experiment, as follows:
| Initial concentration | initial rate of disappearance of |
| Experiment 1 | | |
| Experiment 2 | | |
| Experiment 3 | | |
Since there is only one reactant we assume that the rate law has the form:
$$Rate=k[N_2O_5]^x$$
Where the reaction order can take on any whole number value from, \(x=0,\,1,\,2,...\) We determine the reaction order ( x ) by comparing the ratios of the initial concentration of the reactant (\(N_2O_5\)) in pair-wise experiments to the ratios of the initial rate of disappearance of the reactant.
The initial concentration of (\(N_2O_5\)) in the first experiment is \(1.0X10^{-1}M\), in the second experiment the concentration has been doubled, and in the third experiment, the concentration of \(N_2O_5\) has been quadrupled. We proceed by measuring the first ten seconds or so of the reaction for the three different experiments as the reactant is consumed.
Now, when we compare experiment 1 and experiment 2 by taking the ratio of the initial rates of disappearance of \(N_2O_5\), we get:
$$\frac{Experiment 1:\, initial\, rate\, of\, disappearance,\,N_2O_5}{Experiment 2:\, initial\, rate\, of\, disappearance, \,N_2O_5}=\frac{2.4X10^{-6}M*s^{-1}}{4.8X10^{-6}M*s^{-1}}=2$$
Doing the same for the experiment 2 and experiment 3 pair, we get:
$$\frac{Experiment 2:\, initial\, rate\, of\, disappearance,\,N_2O_5}{Experiment 3:\, initial\, rate\, of\, disappearance, \,N_2O_5}=\frac{4.8X10^{-6}M*s^{-1}}{9.6X10^{-6}M*s^{-1}}=2$$
The initial concentration of N2O5 from experiment 1 to experiment 2 was doubled and the initial concentration of the reactant from experiment 2 to experiment 3 was doubled so we get the following ratios which pertain to the reaction order, x :
$$x=\frac{\frac{Experiment\,1:\, \textbf{initial}\, \textbf{rate}\, of\, disappearance,\,N_2O_5}{Experiment\,2:\,\textbf{inital}\, \textbf{rate}\, of\, disappearance,\,N_2O_5}}{\frac{Experiment\,1:\, \textbf{inital}\, \textbf{concentration},\,N_2O_5}{Experiment\,2:\, \textbf{initial}\, \textbf{concentration}, N_2O_5}}$$
$$x=\frac{\frac{2.4X10^{-6}}{4.8X10^{-6}}}{\frac{1.0X10^{-2}}{2.0X10^{-2}}}=\frac{\frac{1}{2}}{\frac{1}{2}}=1$$
and,
$$x=\frac{\frac{Experiment\,2:\, \textbf{initial}\, \textbf{rate}\, of\, disappearance,\,N_2O_5}{Experiment\,3:\,\textbf{inital}\, \textbf{rate}\, of\, disappearance,\,N_2O_5}}{\frac{Experiment\,2:\, \textbf{inital}\, \textbf{concentration},\,N_2O_5}{Experiment\,3:\, \textbf{initial}\, \textbf{concentration}, N_2O_5}}$$
$$x=\frac{\frac{4.8X10^{-6}}{9.6X10^{-6}}}{\frac{2.0X10^{-2}}{4.0X10^{-2}}}=\frac{\frac{1}{2}}{\frac{1}{2}}=1$$
we obtained the same value for, x, for different pairs of experiments and we can now express the rate law as:
$$Rate=k[N_2O_5]^1$$
we determine that the dimensions for the rate constant, k, for this first-order rate law is, s-1, so the dimensions of Rate will be molarity per second (M•s-1).
Now, we can solve for the rate constant (k) by plugging in the values from any of the above three experiments for the initial rate of reactant consumption, Rate, and the value for the initial concentration of the reactant ([N2O5]) raised to the power of the reaction order. Let's use the values for experiment 2, thus:
$$k=\frac{\textbf{Rate}}{[N_2O_5]^{1}}=\frac{4.8X10^{-6}M\cdot s^{-1}}{2.0X10^{-2}M}=2.4X10^{-4}s^{-1}$$
and so the rate law is:
$$\textbf{Rate}=(2.4X10^{-4}s^{-1})\cdot[N_2O_5]^1$$
Kinetics - Key takeaways
- The change in the concentration of products or reactants per unit time is referred to as the reaction rate.
- The rate of any chemical reaction can be determined by measuring the instantaneous reaction rate.
- The instantaneous rate is the slope of the curve fitted to a scatter plot of the concentration of any one of the reaction components versus time.
- It is important to note that, in general, there is no relationship between the stoichiometric coefficients of balanced reaction and reaction order.
Explanations 
Exams 
Magazine 
