
StudySmarter - The all-in-one study app.
4.8 • +11k Ratings
More than 3 Million Downloads
Free
Americas
Europe



Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persönlichen Lernstatistiken
Jetzt kostenlos anmeldenMechanics and materials are closely connected. Mechanics studies the forces that produce motion, mechanical work, and concepts such as momentum and energy. A classical approach to mechanics includes Newton’s laws of forces interacting in bodies, which can be static or in motion.
The study of materials deals with the properties of solids, focusing on their mechanical properties and how these change depending on the forces interacting with them.
Mechanics is the area of physics that deals with the analysis of bodies, whether static or in motion. Mechanics can be divided into kinematics and dynamics. Kinematics studies the movements and displacement of the body, while dynamics focuses on the forces producing these movements.
Mechanics also studies the changes in the energy of a body in movement as well as the work produced by this object. A large portion of the classical study of dynamics is also dedicated to Newton’s Laws. Sometimes the combination of both is called ‘Newtonian Mechanics’.
The analysis of the changes in velocity, acceleration, or displacement of an object is an integral part of the area of kinematics. For this, objects can move in linear motion (linear kinematics) or circular motion (rotational kinematics). Examples of both can be found below:
Linear kinematicsImagine the movement of a ball over a straight rail or a car on a straight road. Velocity, displacement, or acceleration in these systems occur over just one axis and in only two directions, which simplifies analysis and calculations.
Rotational kinematics Think of the movement of a seat in a carousel or a satellite over the earth. These systems have more complex interactions between the positions and movements of their constituents. As an example, two objects rotating at the same speed around the same centre cover different distances by virtue of being at different distances from the centre. In linear systems, by comparison, two objects at the same speed cover the same distance, even if the directions and axis are not the same.

Rotational kinematics also uses a different set of quantities and a different system of coordinates to make its work easier. While linear kinematics uses a classical 3D cartesian system, rotational kinematics normally uses a cylindrical system or even a spherical one.

For dynamics, the displacement or velocity of a body is not important, but rather how it reacts to changes and why. Newton’s laws of motion are foundational for dynamics. We will introduce them very briefly below.
An object remains in its same state of motion unless it is disturbed by a force.
The rate of change in the momentum (per time) of an object is equal to the force acting on the object.
When two bodies exert forces over each other, the forces are equal in magnitude but have the opposite direction.
The combination of concepts of dynamics and Newton’s laws of forces interacting in bodies allows us to understand systems where multiple forces act on a body or where two bodies interact with each other.
These three concepts are integral to the study of dynamics.
Momentum is the product of the mass of an object and its velocity. When an object accelerates or decelerates, its momentum changes. Momentum is important in the analysis of some interactions where objects exchange energy by impacting each other, as the conservation of momentum applies. One example is an inelastic collision.
In an inelastic collision, the overall momentum of the objects before and after the collisions must be the same.
This is another important concept in mechanics. Objects can have kinetic and potential energy. In most systems, the rule of energy conservation applies, meaning that the total energy of a system is the same before and after something happened within it.
This is the displacement produced by a force. Any work produced is directly linked to the forces moving the object.
Vectors and scalars are two mathematical concepts widely used in mechanics. They allow us to express quantities that only have a magnitude as ‘scalars’, while quantities that have both a magnitude and a direction are known as ‘vectors’.
Vectors are particularly useful in dynamics, as they make it possible for a system of forces interacting with a body to be represented more easily. The representation uses a line along the path the force is being applied and an arrow to indicate its direction. A classic example of vectors and forces is the case of a body moving up a slope.
A car is being pulled up a slope by a security car. The steepness of the slope is 30 degrees. The force of gravity (red arrow) pulls the car down along the vertical direction.

The gravitational force (red arrow) can be split up into two components (yellow arrows), one operating in the perpendicular direction to the slope Fg(y) and the other operating along the slope Fg(x).
The force causes a response Fr(y) from the slope equal in magnitude but opposite in direction (pink arrow). The sum of these forces is zero, leaving Fg(x) as the resulting force pulling the car down the slope. The security car produces a force Fc(x) (blue arrow), pulling the car up the hill.
If the service car’s force Fc(x) is greater than the horizontal component of the gravity Fg(x), the car moves upwards. If Fc(x) is smaller than Fg(x), the car rolls down the hill.
The system of forces can be seen in the equations below:
\(F_y = F_{r(y)} - F_{g(y)}\)
\(F_x = F_{c(x)} - F_{g(x)}\)
If Fx > 0, the car gets pulled up the slope. If Fx < 0, the car rolls down the slope.
The study of materials and their mechanical properties is an important aspect of physics. The properties of a material can tell us how much force an object can withstand and how it will react to the forces acting on it. In mechanics, objects are non-deformable. However, in reality, the forces acting on a body deform and affect it.
Bulk properties are characteristics of any material that are the result of the atoms of that material working together as a ‘bulk’. Properties such as elasticity, density, hardness, and conductivity are all bulk properties.
These arise as part of the internal mechanisms of the atoms that compose an object. Consider elasticity: the reasons why materials are elastic differ. Elasticity in metals is produced by the change in the atomic structure of the material, while in polymers, it is a product of the stretching of the chains that compose the material.
Let’s briefly look at some bulk properties.
Elasticity is defined as the ability of a material to resist deformation after a force is applied to it. The material, in this case, can come back to its original shape or be deformed. Please note that the elasticity of a material has a limit. Any elastic material will deform irreversibly after a certain amount of force is applied.
Hardness is defined as the resistance of a material to being locally deformed, usually demonstrated by making an indentation with a pointy object. An interesting relationship is that sometimes the hardness of a material is inverse to its elasticity. Very often, hard materials are not elastic, and elastic materials are not hard.
Conductivity is defined as the ease with which a material conducts electrical charges. The conductivity is related to the atomic structure of the material.
Within the subject of bulk properties, Young’s modulus is an important characteristic that tells us how easily a material will deform under forces that produce compression or tension.
The formula to calculate the modulus is:
\[E = \frac{\sigma}{\varepsilon}\]
Here, σ is the axial stress or the force per unit of length measured in Pascals, while ε is the proportional deformation equal to the length after the force is applied, divided by the original length of the object.
There is no one measure to know which material is the most elastic. There is, however, an interesting fact that will contradict your notion of elasticity, which is that steel is more elastic than rubber.
Elasticity is the property of a material to resist deformation and return to its original shape. Steel can resist higher forces without deforming irreversibly than rubber or plastics. The most elastic material, in this case, is the stiffest one. (Although it can still deform a little under very large forces.)
They are those properties of any material that are affected by forces that stretch or compress it, or try to break, cut, or deform it. These mechanical properties arise from the bulk properties of a material, which are themselves the results of the interactions between the material’s constituent atoms.
Dynamics is focused on the study of the forces that affect a body and how it reacts to them. Kinematics, on the other hand, studies the trajectory, velocity, and acceleration of a body without taking into account the forces acting on it.
Rotational kinematics is the study of the movement of an object in a circular motion. The study does not take into account the forces exerted on the body.
Flashcards in Mechanics and Materials360
Start learningWhat are materials?
Materials are the substances that an object consists of.
Why does water flow so easily?
The weakness of the water molecules gives water its ability to flow.
How can the forces that bind atoms together modify an object’s properties?
Large forces keep the atoms together, thus producing solids, while small forces or a lack of forces allow liquids to flow.
Do the atoms or molecules of liquids and gases possess a clear structure?
No, they do not possess a clear structure.
What is hardness?
The ability of a material to resist penetration.
Name the hardest known material.
Diamonds.
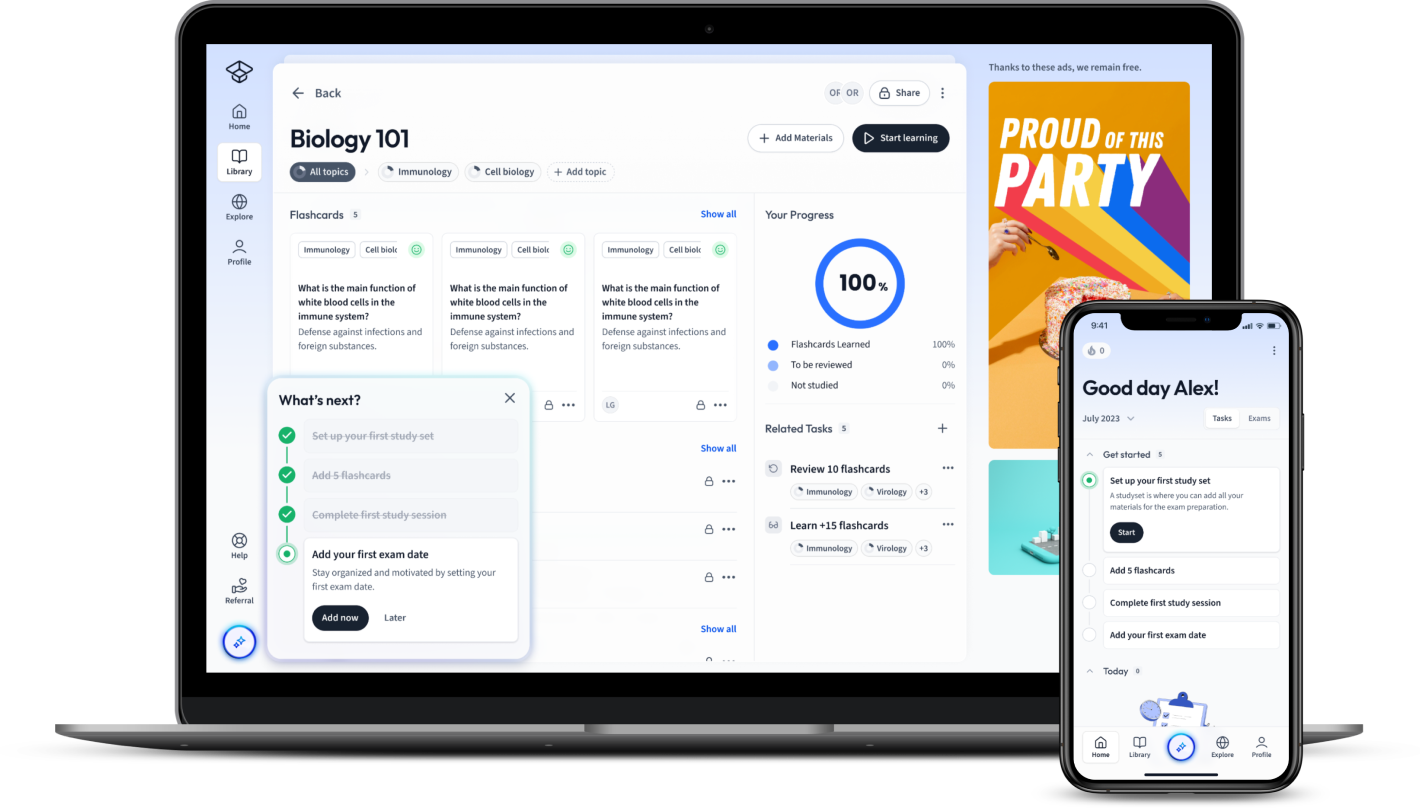
Already have an account? Log in
Open in AppThe first learning app that truly has everything you need to ace your exams in one place
Sign up to highlight and take notes. It’s 100% free.
Save explanations to your personalised space and access them anytime, anywhere!
Sign up with Email Sign up with AppleBy signing up, you agree to the Terms and Conditions and the Privacy Policy of StudySmarter.
Already have an account? Log in