
StudySmarter - The all-in-one study app.
4.8 • +11k Ratings
More than 3 Million Downloads
Free
Americas
Europe



Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persönlichen Lernstatistiken
Jetzt kostenlos anmeldenStatistics is the branch of mathematics used to collect, analyse and present data.
In probability, we explore the idea of independent and dependent events. You will learn about calculating the chance that an event will occur using various methods such as tree and Venn diagrams and conditional and mutually exclusive events.
With Venn diagrams, you can figure out how events can happen at the same time.
Draw a Venn diagram for the following data:
U = numbers under 20
A = even numbers
B = Multiples of 3
Solutions:
Calculate \(P(A \cap B)\)
Solutions:
There are 19 numbers in the entire set.
There are 3 numbers inside the intersection.
So \(P(A \cap B) = \frac{3}{19}\)
Here, we look at sampling, including different methods of sampling and the different types of data. Some people find sampling questions the easiest to answer in an exam, but they can also be quite wordy, so it is important to pay attention – and then you will understand precisely what you are being asked to do.
There are a few different ways to categorize data. We can categorize data as quantitative or qualitative, as well as descriptive and inferential.
There are 400 students in the school, 250 girls and 150 boys. Explain how to take a stratified sample of 40 students in the school.
Solution.
We want to pick 25 girls and 15 boys (so that we have the same proportion as the entire population). One method is to assign all the girls a number from 1-250. Then using a random number generator, generate 25 numbers and then pick those 25 girls.
Repeat the same for the boys: assign them a number from 1-150. Then use your random number generator to generate 15 numbers and then pick those 15 boys.
We need to analyze the data we collect, and the best way to do this is by using measures of location and spread. This enables us to compare data using the following
On a randomly chosen day, each of the 32 students in a class recorded the time (t) in minutes to the nearest minute that it took them to get to school. Find the mean and standard deviation from the following data:
\[\sum t = 1414 \text{ and } \sum t^2 = 69378\]
Solutions:
Mean: \(\frac{\sum t}{n} = \frac{1414}{32} = 44.1875\)
Default Deviation: \(\sqrt{\frac{\sum t^2}{n} - \Big( \frac{\sum t}{n} \Big)^2} = \frac{69378}{32} - (44.1875)^2 = 215.52734375\)
A vital part of statistics is understanding the distribution of data. Distributions are essentially mathematical functions that give the probability that a function will occur. We will look at two main distributions, binomial distribution and normal distribution.
Binomial distribution applies whenever there are two mutually exclusive possible outcomes of an experiment. If an experiment with the probability of the outcome happening being p is performed n times, the probability of this outcome happening n times is:
\(P(X = a) = \left( \begin{array} {c} n \\ a \end{array} \right) p^{a} (1-p)^{n-a}\) with \(\left( \begin{array} {c} n \\ a \end{array} \right) = \frac{n!}{a!(n-a)!}\) (also written as \(^n{C}_a\))A die is tossed 10 times. The outcome of rolling 5 exhibits a binomial distribution: \(X \sim B(10, \frac{1}{6})\). Calculate \(P(X \leq 3)\).
Solution.
This is as simple as calculating P(X = 0), P(X = 1), P(X = 2) and P(X = 3) and summing them all together. Therefore: \(P(X = 0) = \left( \begin{array} {c} 10 \\ 0 \end{array} \right) (\frac{1}{6})^0 (\frac{5}{6})^{10} = 0.1615055829; \quad P(X=1) = \left( \begin{array} {c} 10 \\ 1 \end{array} \right) (\frac{1}{6})^1 (\frac{5}{6})^9 = 0.3230111658; \quad P(X=2) = \left( \begin{array} {c} 10 \\ 2 \end{array} \right) (\frac{1}{6})^2 (\frac{5}{6})^8 = 0.2907100492; \quad P(X=3) = \left( \begin{array} {c} 10 \\ 3 \end{array} \right) (\frac{1}{6})^3 (\frac{5}{6})^7 = 0.155043596\)
Summing all of these together we get: \(P(X \leq 3) = 0.9302721575\)
In some exams, you will have access to a formula booklet with a dedicated section for statistics. Check your exam board's website for this. The most useful formulas are the ones for binomial distribution and mutualistic probability; however, the booklet will also contain statistical tables. You might not need these if you can use a calculator, but they show probability values at significance levels on distributions.
Hypothesis testing involves using distribution to calculate whether or not we can say a statement ( a hypothesis) is true. In the hypothesis testing topic, we will look at conducting one-tailed and two-tailed tests and stating a null hypothesis.
A coffee shop claims that a quarter of the cakes sent to them are missing cherries on top. To test this claim, the number of cakes without cherries in a random sample of 40 is recorded. Using a 5% significance level, find the critical region for a two-tailed test of the hypothesis that the probability of a missing cherry is 0.26.
Solutions:
This is a two-tailed test, meaning we will need to look at both ends. Start at a random number on both ends.
Lower end:
P(X ≤ 6) = 0.07452108246
P(X ≤ 5) = 0.03207217407
P(X ≤ 4) = 0.01136083855
As this is a two-tailed test we want to be as close to 0.025 as possible:
P(X ≤ 4) < 0.025 < P(X ≤ 5).
Upper end:
P(X ≥ 16) = 1 - P(X ≤ 15) = 0.03703627013
P(X ≥ 17) = 1 - P(X ≤ 16) = 0.0171086868649
Again we want to be as close to 0.025 as possible so:
P(X ≥ 17) < 0.025 < P(X ≥ 16)
Our critical regions are therefore P(X ≤ 4) and P(X ≥ 17).
In the representing data topic, we will look at graphical methods to showcase data. These include histograms, box plots and cumulative frequency. We will also look at ways that we can find outliers in data, and how to deal with data anomalies.
If you are studying for A-level exams, some exam boards prove a large data set eg a spreadsheet containing weather data from airports in the UK and around the world. You don't have to memorize any data but what you do have to do is familiarize yourself with the different types of data it contains, and the units of these data.
Statistics is the branch of Mathematics that deals with collecting and analysing numerical data in large quantities.
The three types are descriptive, inferential and quantitative.
Statistical measures to organise, present and summarise data in an informative manner.
Variance is a measure of spread equal to the standard deviation squared.
Flashcards in Statistics1837
Start learningWhat is probability distribution?
A probability distribution is the function that gives the individual probabilities of occurrence of different possible outcomes for an experiment.
What is the sum of all the probabilities of a probability distribution?
1
Identify whether the following requires a discrete or continuous probability distribution?
The amount of rainfall in your city in March.
Continuous
Identify whether the following requires a discrete or continuous probability distribution?
The number of trophies your favourite football club will win this season.
Discrete
Identify whether the following requires a discrete or continuous probability distribution?
The number of students in the class who will pass the mathematics exam.
Discrete
Identify whether the following requires a discrete or continuous probability distribution?
The weight of a newborn baby.
Continuous
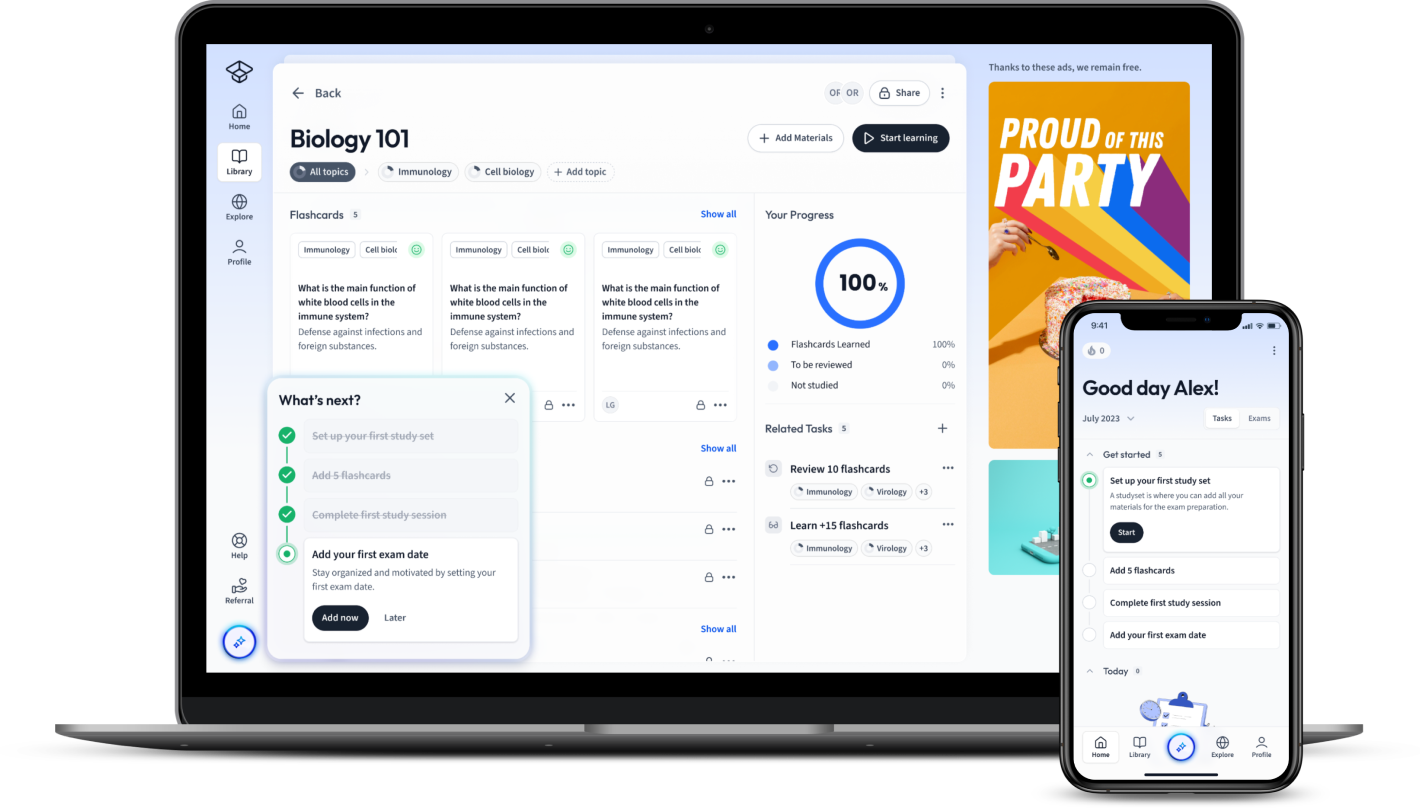
Already have an account? Log in
Open in AppThe first learning app that truly has everything you need to ace your exams in one place
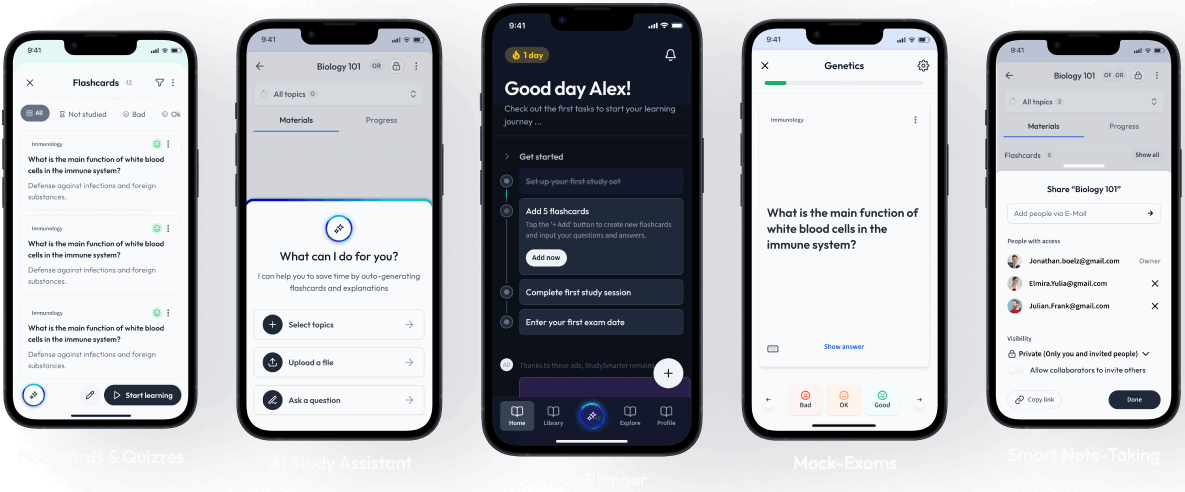
Sign up to highlight and take notes. It’s 100% free.
Save explanations to your personalised space and access them anytime, anywhere!
Sign up with Email Sign up with AppleBy signing up, you agree to the Terms and Conditions and the Privacy Policy of StudySmarter.
Already have an account? Log in